Question

Pete is building a fence around a rectangular field. In his design, the length of the field is 62 feet and the width is 25 feet. The fence includes a gate that measures 9 feet in length.

After Pete builds the fence, he determines that he used 168 feet of fence material, not including the gate. What is the percent error of Pete's design measurements compared to the actual fence material used? Round your answer to the nearest hundredth of a percent.

A. 1.79%
B. 1.82%
C. 3.00%
D. 3.45%

Answer 1

The percentage error is;

A. 1.79%

Explanation:

The given parameters of the rectangular field are;

The length of the field = 62 feet

The width of the field = 25 feet

The width of the gate of the fencing = 9 feet

The actual length of fencing Pete used to fence the field, P₁ = 168 feet

The length of the fencing required in the design, 'P₂' is given as follows;

P₂ = 62 ft. + 62 ft. + 25 ft. + 25 ft. - 9 ft. = 165 ft.

The difference between the actual and design length of fence measurements = P₁ - P₂ = 168 ft. - 165 ft. = 3 ft.

The percentage error in the design measurements compared to the actual fence material used, % Error, is given as follows;

`\% \ Error = (\left | Design \ length - Actual \ length \right | )/(Actual \ length ) * 100`

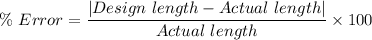
Therefore;

`\% \ Error = (\left | P_1 - P_2 \right | )/(P_2 ) * 100= (\left | 165 - 168 \right |)/(168) * 100 = 1.785 \overline {714285} \%`

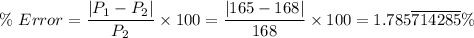
∴ The percentage error of Pete's design measurements compared to the actual fence material used, % Error ≈ 1.79 %.