Question

Help me answer the three questions

A manufacturer makes rectangular blankets in servers style and sizes. The outline of a popular blanket is size A is shown below.


Length = 3x - 7

Width = 2x - 3


A) write a polynomial expression, in simplified form, that represents the perimeter of the blanket. Show work below


B) write a polynomial expression, in the simplest form, that represents the area of the blanket. Show work below


C) the same blanket style in Size B has width 2x + 10 and length 4x - 10. Wrote a polynomial expression, in simplest form that expresses the difference in the areas of blanket a and b. Show work below

Answer 1

A) Perimeter of the blanket = 2(Length + Width)
<=> 2[(3x - 7) + (2x - 3)]

<=> 2(3x - 7 + 2x - 3)
<=> 2(5x - 10)

<=> 10x - 20

B) Area of the blanket = Length * Width

<=> (3x - 7)(2x - 3)

<=>
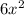`6x^(2)` - 9x - 14x + 21
<=>
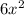`6x^(2)` - 23x + 21

C) Difference between the areas of the two blankets = (L1 * W1) - (L2 * W2)

<=> [(3x - 7)(2x - 3)] - [(2x + 10)(4x - 10)]

<=> (6
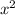`x^(2)` - 23x + 21) - (8
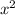`x^(2)` - 20x + 40x - 100)

<=> 6
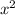`x^(2)` - 23x + 21 - 8
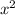`x^(2)` + 20x - 40x + 100

<=> -2
`x^(2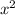)` - 43x + 121

Hope it helps you!