Question

A mass of M1 = 3.25 kg is compressed a distance x1 = 42.0 cm against a spring which has a spring constant of k = 770

N/m as shown below. The mass is released and slides along the smooth horizontal floor (m = 0). After some time, it slides through a rough section of length L = 1.05 m where the coefficient of friction is mk = 0.230. Eventually, the mass reaches the end of floor, slides up a frictionless inclined plane which meets the floor at an angle of a = 36.5°, and at some point stops.
(a) Determine the speed of the mass once it loses contact with the spring.
(b) Calculate the kinetic energy of the mass after it has passed through the rough section of floor.
(c) Determine the distance D up the incline the mass will slide before it comes to a halt.
(d) After stopping on the incline, the mass then slides back down the incline and moves along the floor until it stops by compressing the spring again. Calculate the velocity of the mass just as it reaches the bottom of the incline.
(e) How does the compression distance x2 in the spring after the mass is stopped compare to the compression distance x1 before the mass was released? x2 > x1 ; x2=x1 ; x2

Answer 1

Hi there!

a)
We can begin by using the work-energy theorem. We initially have ALL Spring Potential Energy, which is entirely converted to kinetic energy. Thus:

`E_I = E_F\\\\U = K \\\\(1)/(2)kx^2 = (1)/(2)mv^2`

Rearrange to solve for speed:

`kx^2 = mv^2\\\\v^2 = (kx^2)/(m)\\\\v = \sqrt{(kx^2)/(m)}`

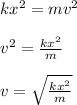
Plug in the values and solve.

`v = \sqrt{(770 * (0.42^2))/(3.25)} = \boxed{6.465 (m)/(s)}`

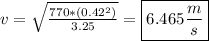
b)
We can find the final kinetic energy by subtracting the work done by friction from the original kinetic energy.

`(1)/(2)mv_i^2 - W_f= (1)/(2)mv_f^2\\\\(1)/(2)mv_i^2 - \mu mgd = K_f`

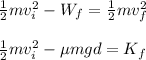
Solve by plugging in values:

`K_f = (1)/(2)(3.25)(6.465^2) - .23(9.8 * 3.25 * 1.05) = \boxed{60.227 J}`

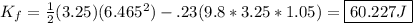
c)
When the mass stops sliding, it will have NO kinetic energy. (All potential). Thus:

`K = U \\\\(1)/(2)mv_f^2 = mgh`

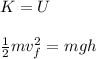
Rearrange and solve for 'h', the VERTICAL distance the block moves up the incline.

`(1)/(2)v_f^2 = gh \\\\h = (v_f^2)/(2g) = 1.89 m`

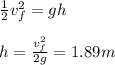
To find 'D', we must use trigonometry to solve.

Recall:

`sin\theta = (O)/(H)\\\\sin\theta = (h)/(D)\\\\D = (h)/(sin\theta) = (1.89)/(sin(36.5)) = \boxed{3.179 m}`

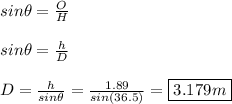
d)

The velocity when the block slides down to its original position will be the SAME as the velocity on its way up, which is 6.09 m/s.

e)

When the block slides all the way down, the block has the same velocity as above.

Therefore, its original kinetic energy is equal to:

`K_i = (1)/(2)mv^2 = (1)/(2)(3.25)(6.09^2) = 60.22 J`

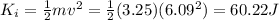
Now, we must calculate its final kinetic energy after some is lost to the friction area.

`K_i - W_f = K_f\\\\60.22 - .230(3.25 * 9.8 * 1.05) = (1)/(2)(3.25)v_f^2\\\\v_f = 5.686 (m)/(s)`

Now, this kinetic energy is converted to elastic potential energy when the block is stopped, so:

`K = U \\\\(1)/(2)mv^2 = (1)/(2)kx^2\\\\mv^2 = kx^2\\\\x = \sqrt{(mv^2)/(k)} = \boxed{.369 m = 36.9 cm}`

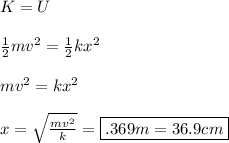
Therefore, x₂ is LESS than x₁, or the resulting compression distance is LESS than the original.