Answer:
Amy is better paid
Explanation:
The mean hourly rate in the department for which Jamie works, μ₁ = $18.80
The standard deviation hourly rate for Jamie's department, σ₁ = $3.20
The mean hourly rate in the department for which Amy works, μ₂ = $17.50
The standard deviation hourly rate for Amy's department, σ₂ = $2.80
The amount Jamie earns, x₁ = $19.75
The amount Amy earns, x₂ = $19.15
The z-score which is the number of sample standard deviation a given value in a sample is above the mean of the sample is given as follows;
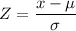
Jamie's standard score, z = (19.75 - 18.80)/3.20 = 0.296875 ≈ 0.3
From the z-table, we get p (z < 0.296875) = 0.61791
Therefore, the probability of earning higher than $19.75 in Jamie's department is p (z >0.296875) = 1 - 0.61791 = 0.38209 or 38.209% earn higher than Jamie
Amy's standard score, z = (19.15 - 17.50)/2.80 ≈ 0.5893
From the z-table, we get p (z > 0.5893) = 1 - 0.71904 = 0.28096
Therefore, the probability of earning higher than $19.15 per hour in Amy's department is 0.28096 or only 28.096% of the people working in Amy's department earn higher than her
Therefore, given that Amy's earns more than 71.904% of the people in her department while Jamie's earns more than 61.791% of the people in his department, Amy is better paid relative to her department's members pay statistics than Jamie.