Solution :
a).
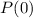 is true
is true
Then ,
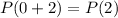 is true.
is true.
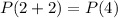 is true
is true
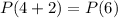 is true.
is true.
Therefore, we see that
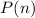 is true for all the even integers :
is true for all the even integers :
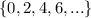
b).
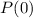 is true
is true
Then ,
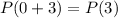 is true.
is true.
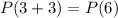 is true
is true
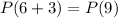 is true.
is true.
Therefore, we see that
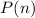 is true for all the multiples of 3 :
is true for all the multiples of 3 :

c).
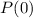 and
and
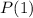 is true, then
is true, then
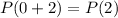 is true
is true
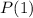 and
and
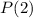 is true, then
is true, then
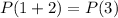 is true.
is true.
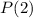 and
and
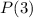 is true, then
is true, then
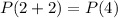 is true.
is true.
So, we observe that
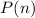 is true for all the non- negative integers :
is true for all the non- negative integers :
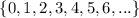 .
.
d).
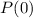 is true,
is true,
So,
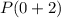 and
and
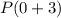 is true or
is true or
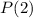 and
and
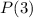 is true.
is true.
Now,
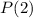 is true.
is true.
Again,
 and
and
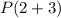 is true or
is true or
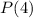 and
and
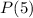 is true.
is true.
Now,
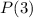 is true.
is true.
Again,
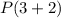 and
and
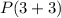 is true or
is true or
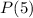 and
and
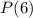 is true.
is true.
Thus,
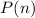 is true for all the non- negative integers except 1 :
is true for all the non- negative integers except 1 :
 .
.