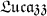Answer:
Explanation:
To solve this question, we can use either of the 2 below given methods:
- Rule of exponents
- Logarithms
1. Rule of Exponents:
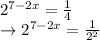
Now, by using the law →
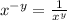 ...
...
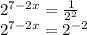
Now, let's take the exponential values as the base values are equal.
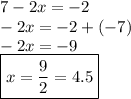
2. Logarithms:
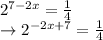
Now, take the logarithm of both the sides of the equation.
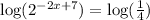
We know that, the logarithm of a number raised to an exponential power is power times the logarithm of the number. So,
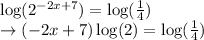
Now, divide both the sides of the equstion by log (2).
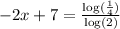
According to the change of base formula,
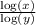 =
=
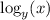 . Then,
. Then,
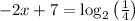
By subtracting 7 from both the sides of the equation & then simplifing it further....
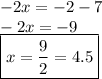
- We get the same value by using either of the 2 methods.
- The value of x = 9/2 or 4.5
_____________
Hope it helps!