Question

a square was altered so that one side is increased by 9 inches and the other side is decreased by 2 inches. the area of the resulting rectangle is 60 square inches. What was the are f the original square.

Answer 1

36 square inches.

Explanation:

Since the original figure was a square, all four side lengths are equivalent. The area for the square will be:

`A=s^2`

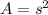
Where s is the length of one side.

One side is increased by nine inches and the other side was decreased by two inches. The area of the resulting rectangle is 60 square inches.

So, one of the new sides is (s + 9).

And the other is (s - 2).

The area with these dimensions is 60. Thus:

`60=(s-2)(s+9)`

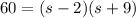
Solve for s. Distribute:

`60=s^2+7s-18`

Isolate the variables:

`s^2+7s-78=0`

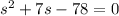
Factor:

`(s+13)(s-6)=0`

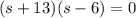
Zero Product Property:

`s+13=0\text{ or } s-6=0`

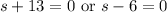
Solve for each case:

`s=-13\text{ or } s=6`

A side length cannot be negative. So, our only solution is:

`s=6\text{ inches}`

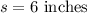
Since each side of the square measures six inches, the area of the original square will be 36 square inches.