Question

5x^2+ 15x – 140 = 0
Solve for x

Answer 1

x = 4, -7

Explanation:

1) Factor out the common term 5.

`5( {x}^(2) + 3x - 28) = 0`

2) Factor x² + 3x - 28.

`5(x - 4)(x + 7) = 0`

3) Solve for x.

x = 4, -7

Therefor, the answer is x = 4, -7.

Answer 2

x = 4, -7

Explanation:

1. Solve the equation using the quadratic formula

The Quadratic formula provides the solution for
`Ax^(2) +Bx+C=0`

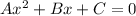
in which A, B, and C are numbers (or coefficients), as follows:

`\frac{-b+\sqrt{b^(2)-4ac } }{2a}`

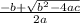
2. Determine the quadratic equation’s coefficients A, B, and C

The coefficients of our equation,
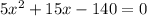`5x^(2) +15x-140=0`, are:

A = 5

B = 15

C = -140

3. Plug these coefficients into the quadratic formula

`\frac{-b+\sqrt{b^(2)-4ac } }{2a}=\frac{-15+\sqrt{15^(2)-4x5x-140 } }{2x5}`

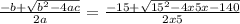
Calculate the expression inside the parentheses.

Simplify exponents and square roots.

`\frac{-15+\sqrt{15^(2)-4x5x-140 } }{2x5}`

`(-15+√(225-4x5x-140 ) )/(2x5)`

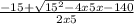
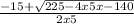
Perform any multiplication or division, from left to right.

`(-15+√(225-20x-140 ) )/(2x5)`

`(-15+√(225-2800 ) )/(2x5)`

`(-15+√(3025) )/(2x5)`

`(-15+√(3025) )/(10)`

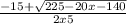
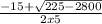
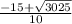
to get the result:

`x=(-15+√(3025) )/(10)`

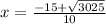
4. Simplify square root

Simplify 3025 by finding its prime factors.

3025

/ \

/ \

5 605

/ \

/ \

5 "121"

/ \

/ \

11 11

The prime factorization of 3025 is 5² • 11²

Write the prime factors.

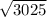`√(3025)` = √5 • 5 • 11 • 11

Group the prime factors into pairs and rewrite in exponent form.

√5 • 5 • 11 • 11 =
`\sqrt{5^(2)x11^(2) }`

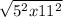
Use rule
`\sqrt{x^(2) }` = x to simplify futher.

`\sqrt{5^(2)x11^(2)}` = 5 • 11

5 • 11 = 55

5. Solve the equation for x

x =
`(-15+55)/(10)`

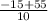
The ± means two answers are possible:

x = 4

or

x = - 7