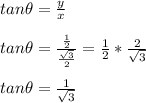Question

What is the value of tangent theta in the unit circle below? One-half StartFraction StartRoot 3 EndRoot Over 3 EndFraction StartFraction StartRoot 3 EndRoot Over 2 EndFraction StartRoot 3 EndRoot

Answer 1

StartFraction StartRoot 3 EndRoot Over 3 EndFraction

Explanation:

I think thats what the answer above meant.

Answer 2

`(1)/(√(3) )`

Explanation:

A unit circle is defined as a circle of unit radius (that is the radius of the circle is equal to 1). In trigonometry, the unit circle is a circle with a radius of 1, while centered at the origin (0, 0) in the Cartesian coordinate.

In the unit circle below, we can see that the line touches the unit circle at point
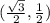`((√(3) )/(2) ,(1)/(2))`, therefore to find the tangent of theta, we use the formula:

`tan\theta = (y)/(x) \\\\tan\theta=((1)/(2) )/((√(3) )/(2) ) =(1)/(2)*(2)/(√(3) ) \\\\tan\theta=(1)/(√(3) )`