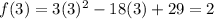Question

Determine whether the quadratic function show below has a minimum or maximum then determine the minimum or maximum value of the function

f(x) = 3x^2 - 18x + 29

Answer 1

The quadratic has a minimum value.

The minimum value is at (3, 2).

Explanation:

We are given the quadratic function:

`f(x)=3x^2-18x+29`

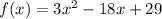
First, since the leading coefficient is positive, this quadratic function will be concave up.

Hence, we will have a minimum value.

The minimum or maximum value is the vertex of the quadratic. The vertex is given by:

`\displaystyle \Big(-(b)/(2a),f\Big(-(b)/(2a)\Big)\Big)`

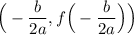
In this case, a = 3, b = -18, and c = 29. Thus, the x-coordinate of the vertex is:

`\displaystyle x=-(-18)/(2(3))=(18)/(6)=3`

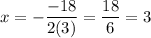
And the minimum value is:

`f(3)=3(3)^2-18(3)+29=2`