Question

A point is reflected in the x-axis. The reflected point is (3,−9). What is the original point? The original point is ( , ). Question 2 What is the distance between the points? The distance between the points is units.

Answer 1

Answer:(3,9) Distance 18 units.

Explanation:

Answer 2

The original point is
`P(x,y) = (3,9)`.

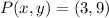The distance between the points is 18 units.

Explanation:

The reflection of a point with respect to the x-axis is defined by the following operation:

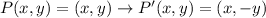`P(x,y) = (x,y) \to P'(x,y) = (x, -y)` (1)

Where:

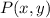`P(x,y)` - Original point.

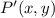`P'(x,y)` - Resulting point.

If we know that
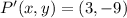`P'(x,y) = (3, -9)`, then the original point is
`P(x,y) = (3,9)`.

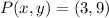The original point is
`P(x,y) = (3,9)`.

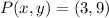The distance between the points (
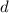`d`), in units, is determined vectorially by the following expression, which is equivalent to the Pythagorean Theorem:

`d = √([P'(x,y) -P(x,y)]\,\bullet\,[P'(x,y) -P(x,y)])`

`d = √((0,18)\,\bullet (0,18))`

`d = \sqrt{0^(2)+18^(2)}`

`d = 18`

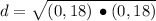
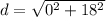
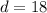
The distance between the points is 18 units.