Question

The Jefferson Valley Bank once had a separate customer waiting line at each teller window, but it now has a single waiting line that feeds the teller windows as vacancies occur. The standard deviation of customer waiting times with the old multiple-line configuration was 1.8 min. Listed below is a simple random sample of waiting times (minutes) with the single waiting line. Use a 0.05 significance level to test the claim that with a single waiting line, the waiting times have a standard deviation less than 1.8 min. What improvement occurred when banks changed from multiple waiting lines to a single waiting line?

Answer 1

There will be sufficient evidence to conclude. A further explanation is provided below.

Explanation:

The given values are:

`\sigma=1.8`

`\alpha=0.05`

`n=10`

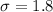
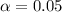
As we know,

`\bar{x}=(\Sigma x_i)/(n)`

`=(71.5)/(10)`

`=7.15`

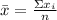
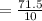
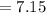
The standard deviation will be:

⇒
`s=\sqrt{(1)/(n-1) \Sigma(x_i- \bar{x})^2 }`

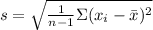
On substituting the values, we get

⇒
`=\sqrt{(1)/(10-1) [(6.5-7.15)^2+...(7.7-7.15)^2]}`

⇒
`=\sqrt{(1)/(9) [(6.5-7.15)^2+...(7.7-7.15)^2]}`

⇒
`=0.477`

According to the question,

Hypotheses:

`H_o: \sigma=1.8`

`H_a: \sigma<1.8`

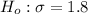
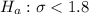
The test statistic will be:

⇒
`X^2=((n-1)s^2)/(\sigma^2)`

⇒
`=((10-1)* 0.477^2)/(1.8^2)`

⇒
`=(2.0477)/(3.24)`

⇒
`=0.632`

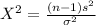
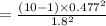
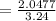
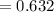
Thus the above is the correct response.