Question

Helene invested a total of $1,000 in two simple-interest bank accounts. One account paid 8% annual interest; the other paid 9% annual interest. The total amount of interest she earned after one year was $86. Enter and solve a system of equations to find the amount invested in each account. Enter the interest rates in order as given in the problem. (Hint: Change the interest rates into decimals first.)

at 9%.

Answer 1

Answer: -600 and 1600 were invested into the two accounts.

Explanation:

x = amount invested in the first account.

y = amount invested in the second account.

You start off with this equation

`x + y = 1000`

`0.08x + 0.09y=86`

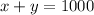
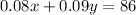
Subtract both sides by y.

`x=1000-y`

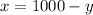
Subsitude 1000 - x for x for the second equation.

`0.08(1000-y)+0.09y=$86`

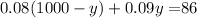
Use the distributive property to solve for y.

`80-0.08y+0.09y=86`

`80-0.01y=86`

`6=-0.01y`

`=-600`

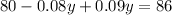
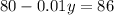
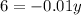
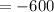
Subsitude -600 for y in the first equation and solve for x.

`x-600=1000`

`x=1600`

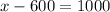
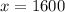
-600 and 1600 were invested into the two accounts.