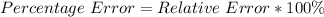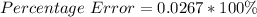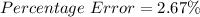Answer:
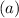
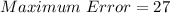
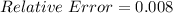
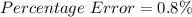
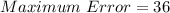
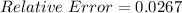
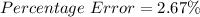
Explanation:
Given
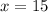 -- edge length
-- edge length
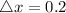 -- possible error
-- possible error
Solving (a): Errors in volume
The volume of a cube is:
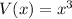
Differentiate
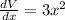
Make dV the subject
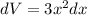
Rewrite as:
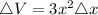
Substitute values for x and
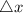
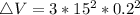
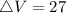
Hence:
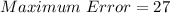
The relative error is then calculated as:
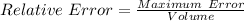
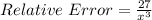
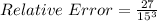
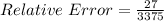
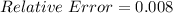
The percentage error is:
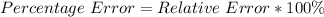
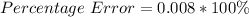
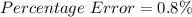
Solving (a): Errors in Surface Area
The volume of a cube is:
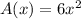
Differentiate
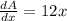
Make dA the subject
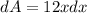
Rewrite as:
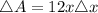
Substitute values for x and
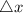
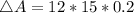
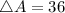
Hence:
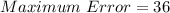
The relative error is then calculated as:
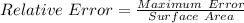
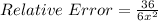
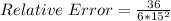
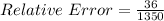
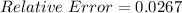
The percentage error is: