Question

What is the height of the tree to the nearest tenth of a foot?

A student wants to measure the height of a tree. From a
point on the ground 10 feet away from the base of the tree,
the angle of elevation to the top of the tree is 65 as
shown. The diagram is not drawn to scale.
feet
7
4
5
QQQQQQQQQQ
QQQQQQQQQQ
0000000000
QQQQQQQQQQ
1
2
0
65
10 feet
Previous

Answer 1

The height of the tree is approximately 21.4 feet

Explanation:

We list out the question parameters first as follows;

The distance from the base of the tree where the angle of elevation is measured, d = 10 feet

The angle of elevation to the top of the tree from 10 feet from the base, θ = 65°

Let 'h' represent the height of the tree, then we have;

The line formed by the angle 65° angle, the height of the tree, 'h', and the distance 'd', form a right triangle with 'h' being the opposite leg to the given reference angle, 65°, and 'd' being the adjacent leg

By trigonometric ratio, we have;

`tan(\theta) = (Opposite \ leg \ length)/(Adjacent\ leg \ length) = (h)/(d)`

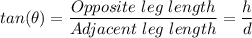
∴ h = d × tan(θ)

Plugging in the given values, we get;

h = 10 feet × tan(65°) = 21 feet
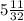`5(11)/(32)` inches

∴ By rounding to the nearest tenth of a foot, the height of the tree, h ≈ 21.4 feet.