Answer:
The distance from the ship to the dock is approximately 5.24 miles
Explanation:
From the parameters given in the question, we have;
The angle formed between the dock and the lighthouse = 70°
The angle formed between the dock and the lighthouse at the ship = 80°
The distance between dock and the lighthouse = 5 miles (From a similar question online)
By sine rule, we have;
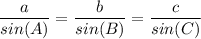
Therefore, we have;


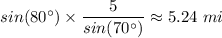
Therefore;
The distance from the ship to the dock ≈ 5.24 miles