Given:
The sequence can be generated by
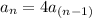
Where
 and
and
 is a whole number greater than 1.
is a whole number greater than 1.
To find:
The first four terms of the given sequence.
Solution:
We have,
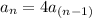 ...(i)
...(i)
It is given that
 . So, for
. So, for
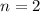 , we get
, we get

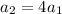

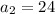
Putting
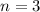 in (i), we get
in (i), we get
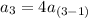
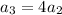
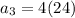
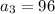
Putting
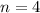 in (i), we get
in (i), we get




The first four terms of the given sequence are 6, 24, 96,384.
Therefore, the correct option is C.