Question

In AABC, MLA = 53, m4C = 84, and side a = 8 inches. Find the length of side b to the nearest tenth of an inch.

Answer 1

6.8 inches

Explanation:

Given data :

m∠ A = 53° , m∠ C = 84° , side a = 8 inches

therefor m ∠ B = ( 180 - (84 + 53 )) = 43°

Find the length of side b

we will apply sine rule here

`(a)/(sinA) = (b)/(sinB) = (c)/(sinC)`

=
`(8)/(sin53)` =
`(b)/(sin43)`

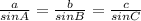
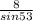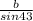
∴ b = ( sin43° * 8 ) / sin53°

= ( 0.6819 * 8 ) / 0.7986

= 5.4552 / 0.7986 = 6.83 ≈ 6.8 inches