Answer:
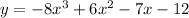
Explanation:
Standard Form of a Polynomial is having an order of numbers with the higher exponents being first and it going lower throughout the order.
ax^2 + bx + c
In this case we have
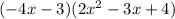 , to get one polynomial all together, multiply the two parenthesis using FOIL.
, to get one polynomial all together, multiply the two parenthesis using FOIL.
FOIL
Front, multiply the first numbers in each parenthesis,
-4x * 2x^2
-8x^3
FOIL
Outer, multiply the first number by the rest of the numbers within the second parenthesis,
-4x * -3x
12x^2
-4x * 4
-16x
At this point, we should have,
-8x^3 + 12x^2 - 16x
FOIL
Inner, multiply the second number by the first number within both parenthesis,
-3 * 2x^2
-6x^2
-8x^3 + 12x^2 - 16x - 6x^2
FOIL
Last, multiply the second number by the rest of the numbers within the second parenthesis,
-3 * -3x
9x
-3 * 4
-12
Now that we finished, you should have,
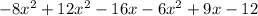
Now combine like terms, meaning adding/subtracting/multiplying/dividing numbers that have the same exponent or variable ending only.
![-8x^2+[12x^2]-16x[-6x^2]+9x-12](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/iyh63uyiwulfjux77nlc.png)

![-8x^2+6x^2 [-16x+9x]-12](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/660dmx25f3veca0thhp9.png)
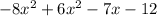
![[y=-8x^2+6x^2 -7x-12]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/29sk4gwxq2dszznlad45.png)
is our answer.