Answer: two times
Explanation:
Given
height of cone A and B
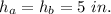
The volume of cone A
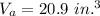
The volume of cone B is 4 times of cone A
the volume of a cone is
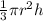
The volume of cone A
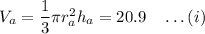
The volume of cone B
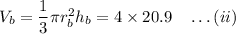
divide (i) and (ii) we get
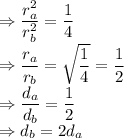
thus, diameter of cone B is twice the diameter of A