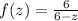Answer:
 for
for
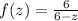
Explanation:
Given
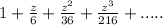
Required
The value at which the series converges
Calculate r
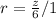
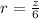
For a series to converge:
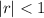
This gives:
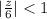
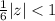
Multiply both sides by 6
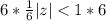

This is calculated using the sum to infinity of a gp.
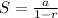
Where
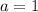
So:
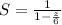
Take LCM
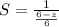
Rewrite as:
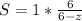
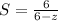
So, the function converges at:
 for
for