Answer:
The correct answer is "$21490".
Step-by-step explanation:
The given expenditures are:
January:
= $205000
September:
= $306000
December:
= $306000
Now,
January average will be:
=
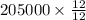
=
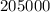 ($)
($)
September average will be:
=
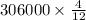
=
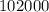
December average will be:
=
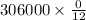
=
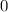
The total average will be:
=
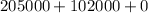
=
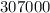 ($)
($)
Hence,
The Interest capitalized for year 2021 will be:
=
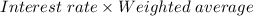
On substituting the estimated values, we get
=
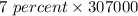
=
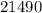 ($)
($)