Question

If 21.00 mL of a 0.68 M solution of C6H5NH2 required 6.60 mL of the strong acid to completely neutralize the solution, what was the final pH at the equivalence point

Answer 1

pH = 2.46

Step-by-step explanation:

Hello there!

In this case, since this neutralization reaction may be assumed to occur in a 1:1 mole ratio between the base and the strong acid, it is possible to write the following moles and volume-concentrations relationship for the equivalence point:

`n_(acid)=n_(base)=n_(salt)`

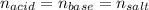
Whereas the moles of the salt are computed as shown below:

`n_(salt)=0.021L*0.68mol/L=0.01428mol`

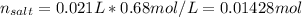
So we can divide those moles by the total volume (0.021L+0.0066L=0.0276L) to obtain the concentration of the final salt:

`[salt]=0.01428mol/0.0276L=0.517M`

Now, we need to keep in mind that this is an acidic salt since the base is weak and the acid strong, so the determinant ionization is:

`C_6H_5NH_3^++H_2O\rightleftharpoons C_6H_5NH_2+H_3O^+`

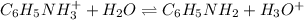
Whose equilibrium expression is:

`Ka=([C_6H_5NH_2][H_3O^+])/(C_6H_5NH_3^+)`

Now, since the Kb of C6H5NH2 is 4.3 x 10^-10, its Ka is 2.326x10^-5 (Kw/Kb), we can also write:

`2.326x10^(-5)=(x^2)/(0.517M)`

Whereas x is:

`x=\sqrt{0.517*2.326x10^(-5)}\\\\x=3.47x10^-3`

Which also equals the concentration of hydrogen ions; therefore, the pH at the equivalence point is:

`pH=-log(3.47x10^(-3))\\\\pH=2.46`

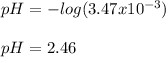
Regards!