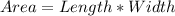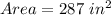Question

Item 19 The staircase has three parallelogram-shaped panels that are the same size. The horizontal distance between each panel is 4.25 inches. What is the area of one panel?

Answer 1

`Area = 287\ in^2`

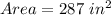
Explanation:

Given

`Length = 20.5`

`Space = 4.25`

`Panels = 3`

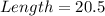
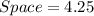
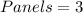
See attachment

Required

The area of one panel

From the attachment, the total width is 50.5in.

i.e.

`Total\ Width = 50.5`

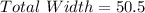
Given that there are 2 spaces between the 3 panels and each space has a length of 4.25 in.

The reduced width is:

`Reduced\ Width = 50.5 - 2 * 4.25`

`Reduced\ Width = 42`

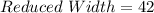
At this point, we can calculate the width of one panel by dividing the reduced width by the number of panels (3).

`Width = (42)/(3)`

`Width = 14`

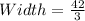
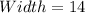
The area of one is:

`Area = Length * Width`

`Area = 20.5 * 14`

`Area = 287\ in^2`