Question

Harold is designing a patio with congruent square concrete tiles. He has 72 tiles. Use grid paper to model all the possible rectangular patios Harold could build. Label the dimensions in units. Which patio has the greatest perimeter? The least perimeter?

Answer 1

(a) The possible dimensions are:

1 unit by 72 units; 2 units by 36 units; 3 units by 24 units; 4 units by 18 units; 6 units by 12 units; 8 units by 9 units

(b): Patio with greatest and the least perimeter

The dimension with the greatest perimeter is: 1 by 72

The dimension with the least perimeter is: 8 by 9

Explanation:

Given

`Tiles = 72`

Solving (a): Possible rectangular models

To do this, we simply list out the possible factor pairs of 72.

So, we have:

1 unit by 72 units; 2 units by 36 units; 3 units by 24 units; 4 units by 18 units; 6 units by 12 units; 8 units by 9 units

Solving (a): Models with the least and the greatest perimeter

Perimeter (P) is calculated using:

`P = 2 * (L + W)`

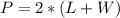
So:

1 unit by 72 units;

`P = 2 *(1 + 72) = 146 units`

2 units by 36 units;

`P = 2 *(2 + 36) = 76 units`

3 units by 24 units;

`P = 2 *(3 + 24) = 54 units`

4 units by 18 units;

`P = 2 *(4 + 18) = 44 units`

6 units by 12 units;

`P = 2 *(6 + 12) = 36 units`

8 units by 9 units

`P = 2 *(8 + 9) = 34 units`

From the calculations above:

The dimension with the greatest perimeter is: 1 by 72

The dimension with the least perimeter is: 8 by 9