Answer:
Let
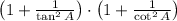 , we proceed to prove the trigonometric expression by trigonometric identity:
, we proceed to prove the trigonometric expression by trigonometric identity:
1)
 Given
Given
2)
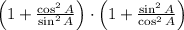
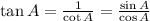
3)
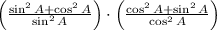
4)
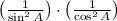
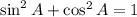
5)
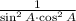
6)
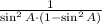
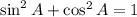
7)
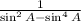 Result
Result
Explanation:
Let
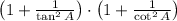 , we proceed to prove the trigonometric expression by trigonometric identity:
, we proceed to prove the trigonometric expression by trigonometric identity:
1)
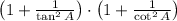 Given
Given
2)
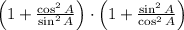
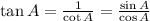
3)
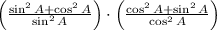
4)
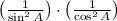
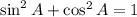
5)
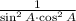
6)
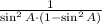
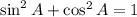
7)
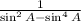 Result
Result