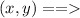Question

What is the answer to a triangle translation where A is (1,4), B is (2,-2) and C is (-3,2) What is the Answer to A

Answer 1

Question:

A translation is applied to the triangle where A(1, 4) , B(2, -2) , and C(-3, 2). The image is the triangle that has vertices ​ A′(5, 4) ​, ​ B′(6, -2) ​​, and C′(1, 2)​.

Answer:

`(x,y) ==>`
`(x + 4,y)`

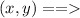
Explanation:

Given

`A = (1,4)\\B = (2,-2)\\C = (-3,2)`

`A' = (5,4)\\B' = (6,-2)\\C' = (1,2)`

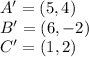
From the translation of triangle ABC to A'B'C',

It will be observed that the y coordinates of both triangle remain unchanged.

This implies that triangle ABC is translated on the x coordinates alone.

Considering the x coordinates of A and A', we have:

`1 + k = 5`

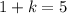
Make k the subject

`k = 5 - 1`

`k = 4`

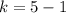
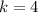
When 4 is added to the x coordinates of B and C, it gives the x coordinates of B' and C'.

Hence, the rule of translation is:

`(x,y) ==>`
`(x + 4,y)`