Question

Please solve the following sum or difference identity.

You are given that
`\displaystyle\sin(A) = (24)/(25)`, with
`A` in Quadrant I, and
`\displaystyle\sin(B) = -(4)/(5)`, with
`B` in Quadrant IV. Find
`\sin(A-B)`. Give your answer as a fraction.

Answer 1

`\mathsf {sin (A - B) =(4)/(5) }`

Explanation:

`\textsf {Trigonometric Identities to keep in mind :}`

1. 
   `\mathsf {sin (A - B) = sinAcosB - cosAsinB}`
2. 
   `\mathsf {sin \theta = opposite/hyporenuse}`
3. 
   `\mathsf {cos \theta = adjacent/hypotenuse}`

`\textsf {To find cos A and cos B, we can use the Pythagorean Theorem} \\\textsf {to find the missing sides so we can take the ratio.}`

`\textsf {Finding the adjacent side of angle A :}`

`\implies \mathsf {24^(2) + x^(2) = 25^(2) }`

`\implies \mathsf {x^(2) = 625 - 576 }`

`\implies \mathsf {\sqrt{x^(2) } = √(49) }`

`\implies \mathsf {x = 7}`

`\textsf {Hence, cos A will be :}`

`\implies \textsf {cosA = 7/25 (as cos is positive in the 1st Quadrant)}`

`\textsf {Finding the adjacent side of angle B :}`

`\implies \mathsf {4^(2) + x^(2) = 5^(2) }`

`\implies \mathsf {x^(2) = 25 - 16 }`

`\implies \mathsf {\sqrt{x^(2) } = √(9) }`

`\implies \mathsf {x = 3}`

`\textsf {Hence, cos B will be :}`

`\implies \textsf {cos B = 3/5 (as cos is positive in the 4th quadrant)}`

`\textsf {Finding sin (A - B) :}`

`\implies \mathsf {sin (A - B) = ((24)/(25) * (3)/(5)) - ((7)/(25) * -(4)/(5)) }`

`\implies \mathsf {sin (A - B) = (72)/(125) + (28)/(125)}`

`\implies \mathsf {sin (A - B) = (100)/(125) = (4)/(5) }`

Answer 2

`sin(A - B) = (4)/(5)`

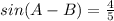
Explanation:

Given:

`sin(A) = (24)/(25)`

`sin(B) = -(4)/(5)`

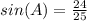
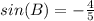
Need:

`sin(A - B)`

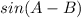
First, let's look at the identities:

sum:
`sin(A + B) = sinAcosB + cosAsinB`

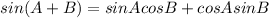
difference:
`sin(A - B) = sinAcosB - cosAsinB`

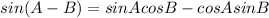
The question asks to find sin(A - B); therefore, we need to use the difference identity.

Based on the given information (value and quadrant), we can draw reference triangles to find the simplified values of A and B.

sin(A) =
`(24)/(25)`

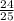
cos(A) =
`(7)/(25)`

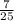
sin(B) =
`-(4)/(5)`

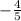
cos(B) =
`(3)/(5)`

Plug these values into the difference identity formula.

`sin(A - B) = sinAcosB - cosAsinB`

`sin(A - B) = ((24)/(25))((3)/(5)) - (-(4)/(5))((7)/(25))`

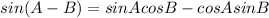
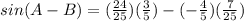
Multiply.

`sin(A - B) = ((72)/(125)) + ((28)/(125))`

Add.

`sin(A - B) = (4)/(5)`

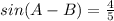
This is your answer.

Hope this helps!