Answer:
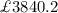
Explanation:
Let P denotes principal amount, T denotes time period and R denotes rate of interest.
Amount =
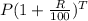
Amir pits £3035 into a bank account. The account pays 4% compound interest each year.
Put
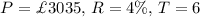
Amount =
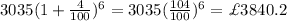
Therefore, Amir will have
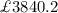 in the account after 6 years.
in the account after 6 years.