Question

Richard has just been given an l0-question multiple-choice quiz in his history class. Each question has five answers, of which only one is correct, Since Richard has not attended a class recently, he doesn't know any of the answers, Assuming that Richard guesses on all 10 questions. Find the indicated probabilities.

A) What is the probability that he will answer all questions correctly?
B) What is the probability that he will answer all questions incorrectly?
C) What is the probability that he will answer at least one of the questions correctly?
Then use the fact that P(r1) = 1 P(r = 0).
D) What is the probability that Richard will answer at least half the questions correctly?

Answer 1

a) 0.0000001024 probability that he will answer all questions correctly.

b) 0.1074 = 10.74% probability that he will answer all questions incorrectly

c) 0.8926 = 89.26% probability that he will answer at least one of the questions correctly.

d) 0.0328 = 3.28% probability that Richard will answer at least half the questions correctly

Explanation:

For each question, there are only two possible outcomes. Either he answers it correctly, or he does not. The probability of answering a question correctly is independent of any other question. This means that we use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
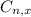`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

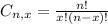
And p is the probability of X happening.

Each question has five answers, of which only one is correct

This means that the probability of correctly answering a question guessing is
`p = (1)/(5) = 0.2`

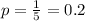
10 questions.

This means that
`n = 10`

A) What is the probability that he will answer all questions correctly?

This is
`P(X = 10)`

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 10) = C_(10,10).(0.2)^(10).(0.8)^(0) = 0.0000001024`

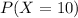
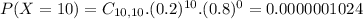
0.0000001024 probability that he will answer all questions correctly.

B) What is the probability that he will answer all questions incorrectly?

None correctly, so
`P(X = 0)`

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(10,0).(0.2)^(0).(0.8)^(10) = 0.1074`

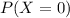
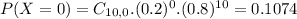
0.1074 = 10.74% probability that he will answer all questions incorrectly

C) What is the probability that he will answer at least one of the questions correctly?

This is

`P(X \geq 1) = 1 - P(X = 0)`

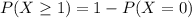
Since
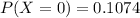`P(X = 0) = 0.1074`, from item b.

`P(X \geq 1) = 1 - 0.1074 = 0.8926`

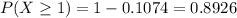
0.8926 = 89.26% probability that he will answer at least one of the questions correctly.

D) What is the probability that Richard will answer at least half the questions correctly?

This is

`P(X \geq 5) = P(X = 5) + P(X = 6) + P(X = 7) + P(X = 8) + P(X = 9) + P(X = 10)`

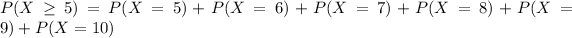
In which

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 5) = C_(10,5).(0.2)^(5).(0.8)^(5) = 0.0264`

`P(X = 6) = C_(10,6).(0.2)^(6).(0.8)^(4) = 0.0055`

`P(X = 7) = C_(10,7).(0.2)^(7).(0.8)^(3) = 0.0008`

`P(X = 8) = C_(10,8).(0.2)^(8).(0.8)^(2) = 0.0001`

`P(X = 9) = C_(10,9).(0.2)^(9).(0.8)^(1) \approx 0`

`P(X = 10) = C_(10,10).(0.2)^(10).(0.8)^(0) \approx 0`

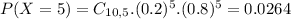
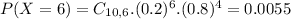
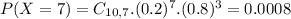
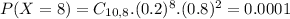
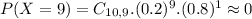
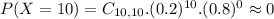
So

`P(X \geq 5) = P(X = 5) + P(X = 6) + P(X = 7) + P(X = 8) + P(X = 9) + P(X = 10) = 0.0264 + 0.0055 + 0.0008 + 0.0001 + 0 + 0 = 0.0328`

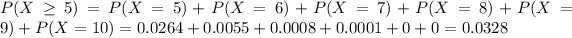
0.0328 = 3.28% probability that Richard will answer at least half the questions correctly