If the 0's are indeed zeroes, then it would appear that you're using degrees, so that the equation
r(θ) = 2 sin(0°) + 3 sin(90°)
describes a circle r = 3 (since sin(0°) = 0 and sin(90°) = 1). In this case, the area would simply be π r ² = 9π.
But I suspect you meant to use θ, so the curve has the far more interesting equation,
r(θ) = 2 sin(θ) + 3 sin(9θ)
Since sin(9θ) has a period of 2π/9 and sin(θ) has a period of 2π, their sum has a period of 2π. (That is, 2π times the LCM of 1 and 1/9, which is 1.) But we observe r(θ) is odd, since
r(-θ) = 2 sin(-θ) + 3 sin(-9θ)
… = -2 sin(θ) - 3 sin(9θ)
… = - r(θ)
which tells us that the curve closes itself over a half-period. So the area bounded by the curve is given by the integral,
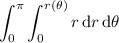
If you're not familiar with double integrals yet, all you need to know is that this reduces to the area formula you may/should be familiar with,

Compute the integral:
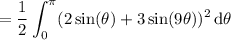

Apply some identities:
sin²(θ) = (1 - cos(2θ)) / 2
sin(θ) sin(9θ) = (cos(9θ - θ) - cos(9θ + θ)) / 2 = (cos(8θ) - cos(10θ)) / 2
sin²(9θ) = (1 - cos(18θ)) / 2
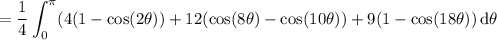
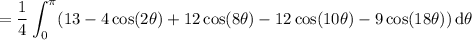
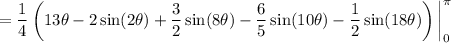

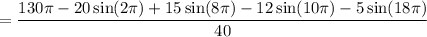
= 13π/4