Question

A 20 Kg bike is moving at 6 m/s down a hill. What is the momentum of the bike?
Show your work

Answer 1

Step-by-step explanation:

Newton's first law of motion states that every object will remain at rest or in uniform motion in a straight line unless acted upon by a net external force. In other words, when no net force acts on an object, the acceleration of the object is zero. Hence, the tendency of an object to resist any change in its velocity is known as inertia.

In an inertial reference frame (frame of reference in which Newton's first law of motion is true), mass is defined as a quantitative measurement of the concept of inertia, where the larger the mass of an object, the greater the inertia of the object (greater tendency to resist change in the state of motion).

Additionally, Newton's second law of motion, in his work Philosophiae Naturalis Principia Mathematica (1687), was originally defined as the rate of change of the momentum of a particle is equivalent to the net force acting on the particle and is in the direction of the force. This can be expressed as the differential equation

`\vec{F}_(net) \ = \ \displaystyle\frac{d\textit{\textbf{p}}}{dt}`.

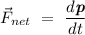But what is momentum?

We know that a moving object has momentum. This is the tendency of the object to keep moving in the same direction unless acted on by an external force (do not confuse this with the definition of inertia). Simply put, momentum can be imagined as the quantitative measure of how "unstoppable" is an object in motion.

Formally, momentum,
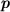`\textbf{\textit{p}}`, is defined as the product of the mass of an object and its velocity.

`\textbf{\textit{p}} \ = \ m\textbf{\textit{v}}`.

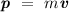Following the mathematical definition of momentum, the differential equation shown above can the be rewritten to yield the modern definition of the second law of motion that we know today,

`\vec{F}_(net) \ = \ \displaystyle\frac{d(m \ * \ \textit{\textbf{v}})}{dt} \\ \\ \vec{F}_(net) \ = \ m\displaystyle\frac{d\textit{\textbf{v}}}{dt} \\ \\ \vec{F}_(net) \ = \ m\textit{\textbf{a}}`

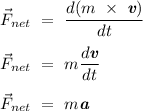
Notice that momentum does not just depend on the object's mass (scalar quantity), but also the velocity (vector quantity) of the object in which it is traveling. Hence, the momentum of an object is also dependent on its direction, implying that momentum changes when

• The speed of the object changes
• The direction of the object changes.

To calculate the momentum of the bike, substitute the known quantities into the formula of momentum.

`\textbf{\textit{p}} \ = \ (20 \ \text{kg})(6 \ \text{m s}^(-1)) \\ \\ \textbf{\textit{p}} \ = \ 120 \ \text{kg m s}^(-1)`

Answer 2

`\boxed {\boxed {\sf 120 \ kg*m/s \ down \ the \ hill}}`

Step-by-step explanation:

Momentum is the quantity of motion of a moving object. It is the product of mass and velocity.

`p=mv`

The mass of the bike is 20 kilograms. The velocity is 6 meters per second.

`p= 20 \ kg * 6 \ m/s`

Multiply.

`p= 120 \ kg*m/s`

Momentum is a vector quantity, so it has both magnitude and direction. The direction of the momentum is in the direction of the velocity. The velocity is down the hill, so the momentum is also down the hill.

The bike's momentum is 120 kg*m/s down the hill.