Question

Log2 (X^2+3x+2)=1 state the universe and solve each of the following for x.​

Answer 1

By "state the universe" I suppose you mean "domain". log₂(x ² + 3x + 2) is defined for

x ² + 3x + 2 = (x + 1) (x + 2) > 0 → x < -2 or x > -1

(To solve the inequality, consider values of x between the ones that make the expression exactly equal to 0, in this case x = -2 and x = -1. We have, for instance, for x = -3, that (-3)² + 3(-3) + 2 = 2 > 0, so x ² + 3x + 2 > 0 for all x < -2.)

Now solve the equation: Write both sides as powers of 2 to eliminate the logarithm on the left:

`\log_2(x^2+3x+2)=1\implies 2^(\log_2(x^2+3x+2))=2^1\implies x^2+3x+2=2`

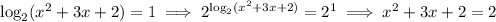
Solve the remaining quadratic:

x ² + 3x + 2 = 2

x ² + 3x = 0

x (x + 3) = 0

x = 0 or x = -3

Both of these solutions are within the presribed domain (-3 < -2 and 0 > -1), so we're done.