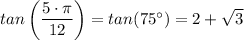Answer:
1)
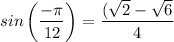
2)
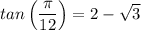
3)
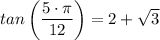
Explanation:
1)
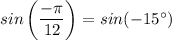
sin(-15°) = sin(30° + (- 45°)) = sin(30°)cos(-45°) + cos(30°)sin(-45°)
sin(30°)cos(-45°) + cos(30°)sin(-45°) = 1/2 × (√2)/2 + (√3)/2 × (-√2)/2
1/2 × √2/2 + √3/2 × -√2/2 = (√2)/4 - (√6)/4 = ((√2) - (√6))/4
sin(-15°) = ((√2) - (√6))/4
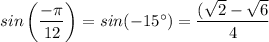
2)
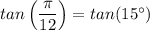
tan(15°) = tan(45° + (-30°)) = (tan(-30°) + tan(45°))/(1 - tan(-30°)×tan(45°))
(tan(-30°) + tan(45°))/(1 - tan(-30°)×tan(45°)) = ((-1/√3) + 1)/(1 - (-1/√3))
((-1/√3) + 1)/(1 - (-1/√3)) = (3 - √3)/(3 + √3) = (3 - √3)·(3 -√3)/((3 - √3)·(3 + √3))
(3 - √3)·(3 -√3/((3 - √3)·(3 + √3)) = (9 - 6·√3 + 3)/(9 - 3) = (12 - 6·√3)/6
(2 - √3)
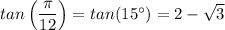
3)
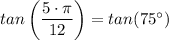
tan(75°) = tan(30° + 45°) = (tan(30°) + tan(45°))/(1 - tan(30°)×tan(45°))
(tan(30°) + tan(45°))/(1 - tan(30°)×tan(45°)) = ((1/√3) + 1)/(1 - 1/√3)
((1/√3) + 1)/(1 - 1/√3) = (3 + √3)/(3 - √3) = (3 + √3)·(3 +√3/((3 - √3)·(3 + √3))
(3 + √3)·(3 +√3/((3 - √3)·(3 + √3)) = (9 + 6·√3 + 3)/(9 - 3) = (12 + 6·√3)/6
(12 + 6·√3)/6 = 2 + √3