Answer:

Explanation:
The formula for slope is:
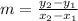
where (x₁, y₁) and (x₂, y₂) are the points on the line.
We are given the points (-3,1) and (-1,5). Therefore,
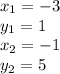
Substitute the values into the formula.
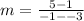
Solve the numerator.
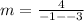
Solve the denominator.
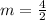
Divide.
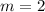
The slope of the line is 2.