Answer:
Volume of the given pyramid = 1122.37 cubic feet
Explanation:
Volume of the regular hexagonal pyramid =
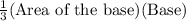
Measure of internal angle of a polygon =
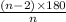
Here, n = number of sides of the polygon
For a hexagon, n = 6
Measure of interior ∠C =
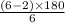
= 120°
Measure of ∠BCD =
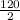
= 60°
By applying tangent rule in ΔCED,
tan(∠ECD) =

tan(60°) =
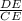
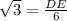
DE =
 feet
feet
And cos(60°) =
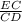

CD = 12 feet
Area of ΔBCD =
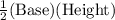
=
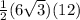
=
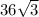 feet
feet
Area of hexagonal Base of the pyramid =
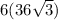
= 216√3 square feet
Since, lateral height of the pyramid (AC) = 15 feet
By applying Pythagoras theorem in ΔADC,
AC² = AD² + CD²
(15)² = AD² + (12)²
AD =
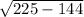
AD = 9 feet
Volume of the given pyramid =
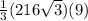
= 648√3 cubic feet
= 1122.37 cubic feet