Question

Find area of the shaded region.

Area of addition and subtraction, trigonometry, and sohcahtoa.

I’ve wasted many pints asking, please I ask kindly that no one puts fake answers, I truly need help with these problems and it is inconsiderate of those who post an answer for points so please respect others.

Answer 1

The area of the shaded region is about 38.1 square centimeters.

Explanation:

We want to find the area of the shaded region.

To do so, we can first find the area of the sector and then subtract the area of the triangle from the sector.

The given circle has a radius of 6 cm.

And the given sector has a central angle of 150°.

The area for a sector is given by the formula:

`\displaystyle A=\pi r^2\cdot (\theta)/(360^\circ)`

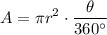
In this case, r = 6 and θ = 150°. Hence, the area of the sector is:

`\displaystyle \begin{aligned}A&=\pi(6)^2\cdot (150)/(360)\\ &=36\pi\cdot (5)/(12)\\&=3\pi \cdot 5\\&=15\pi \text{ cm}^2\end{aligned}`

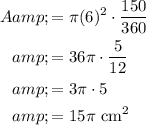
Now, we can find the area of the triangle. We can use an alternative formula:

`\displaystyle A=(1)/(2)ab\sin(C)`

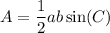
Where a and b are the side lengths, and C is the angle between them.

Both side lengths of the triangle are the radii of the circle. So, both side lengths are 6.

And the angle C is 150°. Hence, the area of the triangle is:

`\displaystyle A=(1)/(2)(6)(6)\sin(150)=18\sin(150)`

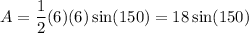
The area of the shaded region is equivalent to the sector minus the triangle:

`A_{\text{shaded}}=A_{\text{sector}}-A_{\text{triangle}}`

Therefore:

`A_{\text{shaded}}=15\pi -18\sin(150)`

Use a calculator:

`A_{\text{shaded}}=38.1238...\approx 38.1\text{ cm}^2`

The area of the shaded region is about 38.1 square centimeters.