Answer:
![\displaystyle \int\limits^1_0 {[2f(x) - g(x)]} \, dx = 11](https://img.qammunity.org/2022/formulas/mathematics/high-school/m8jcdcoxtv40knv831uvv9vqjz6lkk83xr.png)
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Algebra I
- Functions
- Function Notation
Calculus
Integrals
Integration Property [Multiplied Constant]:
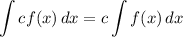
Integration Property [Addition/Subtraction]:
![\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/r5yh324r81plt97j3zrr5qi2xxczxlqi34.png)
Explanation:
Step 1: Define
Identify
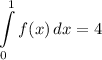
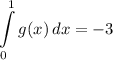
![\displaystyle \int\limits^1_0 {[2f(x) - g(x)]} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/sipo330cbxu9tbw00uyew0u0lakb2zdpa4.png)
Step 2: Find
- [Integral] Rewrite [Integration Property - Subtraction]:
![\displaystyle \int\limits^1_0 {[2f(x) - g(x)]} \, dx = \int\limits^1_0 {2f(x)} \, dx - \int\limits^1_0 {g(x)} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/2hzo8xwiiymui2phkxod9l51hgqf056w4o.png)
- [1st Integral] Rewrite [Integration Property - Multiplied Constant]:
![\displaystyle \int\limits^1_0 {[2f(x) - g(x)]} \, dx = 2\int\limits^1_0 {f(x)} \, dx - \int\limits^1_0 {g(x)} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/21ohywzbyhaqd3jbgxxgka73u423qnponf.png)
- Substitute in integral values:
![\displaystyle \int\limits^1_0 {[2f(x) - g(x)]} \, dx = 2(4) - (-3)](https://img.qammunity.org/2022/formulas/mathematics/high-school/4sxbnu6tiloljpjzxs9gi9g1cm48tyecnh.png)
- Multiply:
![\displaystyle \int\limits^1_0 {[2f(x) - g(x)]} \, dx = 8 - (-3)](https://img.qammunity.org/2022/formulas/mathematics/high-school/fnbrgvo5rc9djp2ejiwqhp5aupc1f1947h.png)
- Subtract:
![\displaystyle \int\limits^1_0 {[2f(x) - g(x)]} \, dx = 11](https://img.qammunity.org/2022/formulas/mathematics/high-school/m8jcdcoxtv40knv831uvv9vqjz6lkk83xr.png)
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Integration
Book: College Calculus 10e