Solution :
Acceleration due to gravity of the earth, g

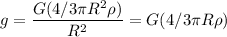
Acceleration due to gravity at 1000 km depths is :
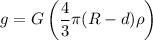
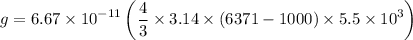
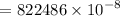
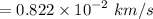
= 8.23 m/s
Acceleration due to gravity at 2000 km depths is :
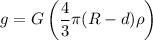
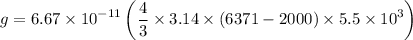
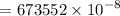
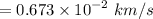
= 6.73 m/s
Acceleration due to gravity at 3000 km depths is :
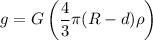
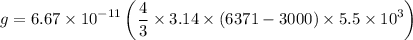
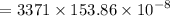
= 5.18 m/s
Acceleration due to gravity at 4000 km depths is :
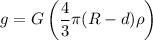
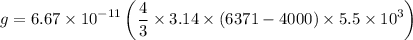
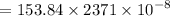
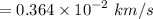
= 3.64 m/s