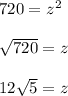Question

Kami's bird is on the

ground. He is 12 feet

away from a free and the

tree is 24 feet tall. The

bird flies to reach the top

of the tree. How far did

the bird have to fly?

Answer 1

The bird had to fly
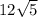`12√(5)` feet to reach the top.

Explanation:

Assuming that the tree is perpendicular to the ground, then the given problem forms a right triangle. The tree's height is one of the legs (sides of the right triangle that is adjacent to the right angle), and the distance that Kami is from the tree is the other leg. The distance from where Kami is to the top of the tree is the hypotenuse (side of the right triangle that is opposite from the right angle). Since this is a right triangle, one can apply the Pythagorean theorem. The Pythagorean theorem states;

`x^2 + y^2 = z^2`

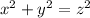
Where (x) and (y) are the legs, and (z) is the hypotenuse. One can substitute in the given values from the problem, and solve for the hypotenuse.

`x^2 + y^2 = z^2`

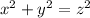
Substitute

`12^2 + 24^2 = z^2\\`

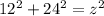
Simplify,

`144 + 576 = z^2\\\\720 = z^2`

Inverse operations,

`720 = z^2\\\\√(720)=z\\\\12√(5)=z`

Answer 2

Kami's bird had to fly 26.8 feet

Explanation: