Question

To teach you how to find the parameters characterizing an object in a circular orbit around a much heavier body like the earth.

The motivation for Isaac Newton to discover his laws of motion was to explain the properties of planetary orbits that were observed by Tycho Brahe and analyzed by Johannes Kepler. A good starting point for understanding this (as well as the speed of the space shuttle and the height of geostationary satellites) is the simplest orbit--a circular one. This problem concerns the properties of circular orbits for a satellite orbiting a planet of mass M. For all parts of this problem, where appropriate, use G for the universal gravitational constant.
1. Find an expression for the square of the orbital period.
2. The quantities v, K, U, and L all represent physical quantities characterizing the orbit that depend on radius R. Indicate the exponent (power) of the radial dependence of the absolute value of each.

Answer 1

a) T² = (
`(4\pi ^2)/(GM)`) r³

b) veloicity the dependency is the inverse of the root of the distance

kinetic energy depends on the inverse of the distance

potential energy dependency is the inverse of distance

angular momentum depends directly on the root of the distance

Step-by-step explanation:

1) for this exercise we will use Newton's second law

F = ma

in this case the acceleration is centripetal

a = v² / r

the linear and angular variable are related

v = w r

we substitute

a = w² r

force is the universal force of attraction

F =
`G (m M)/(r^2)`

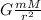
we substitute

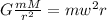
`G (m M)/(r^2) = m w^2 r`

w² =
`(GM)/(r^3)`

angular velocity is related to frequency and period

w = 2π f = 2π / T

we substitute

`( (2\pi )/(T) ) = (GM)/(r^3)`

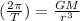
the final equation is

T² = () r³

b) the speed of the orbit can be found

v = w r

v =
`\sqrt{(GM)/(r^3) } \ r`

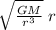
v =
`\sqrt{(GM)/(r) }`

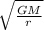
in this case the dependency is the inverse of the root of the distance

Kinetic energy

K = ½ M v²

K = ½ M GM / r

K = ½ GM² 1 / r

the kinetic energy depends on the inverse of the distance

Potential energy

U =

U = -G mM / r

dependency is the inverse of distance

Angular momentum

L = r x p

for a circular orbit

L = r p = r Mv

L =

L =

The angular momentum depends directly on the root of the distance