Answer:
a) The point estimate is 6995.
b) The margin of error is of 1691.
c) The standard error is of 1000
Explanation:
a. Determine the point estimate for the prediction of student expenditures at a university with a graduation rate of 40%.
The point estimate is the mean of the two bounds of the confidence interval. So

The point estimate is 6995.
b. Calculate the margin of error.
The margin of error is the difference between the bounds and the point estimate. So
M = 8686 - 6995 = 6995 - 5304 = 1691
The margin of error is of 1691.
c. Calculate the standard error of the prediction of student expenditures at a university with a graduation rate of 40%.
Now I have to expand a bit into the confidence interval.
We have that to find our
 level, that is the subtraction of 1 by the confidence interval divided by 2. So:
level, that is the subtraction of 1 by the confidence interval divided by 2. So:
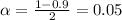
Now, we have to find z in the Ztable as such z has a pvalue of
 .
.
That is z with a pvalue of
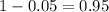 , so Z = 1.645.
, so Z = 1.645.
The margin of error is:
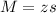
In which s is the margin of error.
We have that M = 1691. So
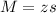

The standard error is of 1000