Question

The decomposition of ethylene oxide (CH₂)₂O(g) → CH₄(g) + CO(g) is a first order reaction with a half-life of 58.0 min at 652 K. The activation energy of the reaction is 218 kJ/mol. Calculate the half-life at 623 K.

Answer 1

`t_(1/2)=375.5min`

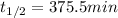
Step-by-step explanation:

Hello!

In this case, since this problem refers to two different temperatures, it is possible to compute the rate constant at 652 K given the half-life at such temperature:

`k=(ln(2))/(58.0 min)=0.0120min^(-1)`

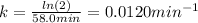
Next, by using the T-variable version of the Arrhenius equation, we can compute the rate constant at 623 K:

`ln((k_2)/(k_1) )=-(Ea)/(R)((1)/(T_2)-(1)/(T_1) ) \\\\ln((k_2)/(k_1) )=-(218000J/mol)/(8.3145(J)/(mol*K))((1)/(623K)-(1)/(652K))\\\\ln((k_2)/(k_1) )=-1.872\\\\k_2=0.0120min^(-1)exp(-1.872)\\\\k_2=0.00185min^(-1)`

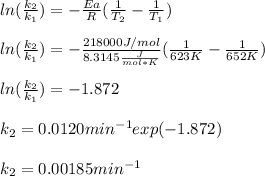
Finally, the half-life at 623 K turns out to be:

`t_(1/2)=(ln(2))/(0.00185min^(-1)) \\\\t_(1/2)=375.5min`

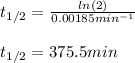
Best regards!