Answer: "
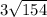 " ;
" ;
or, write as: " 37.229 " .
__________
Explanation:
The digits of "1386" ;
add up to: " (1 + 3 + 8 + 6) " ;
= " (1 + 3) + 8 + 6 " ;
= " (4) + 8 + 6 ;
= " (4 + 8 + 6) " ;
= " (4 + 8) + 6) " ;
= " (12) + 6 "
= "18 " ;
"18" is divisible ("evenly") ; by both: "2" : {" 18 ÷ 2 = 9 ".} ;
and by: "3" : {" 18 ÷ 3 = 6 ".}
Note: If a number is "evenly divisible by both: "2" and "3" ; then said number is divisible by "6" ;
_________
Other: If the sum of the digits of a number result in a number that is evenly divisible by "9" ; then said number is evenly divisible by "9" ;
_________
The sum of the digits of "1386" is: "18" ;
and: the sum of the digits of: "18" ; ⇒ " 1 + 8 = 9" .
{and: " 9 ÷ 9 = 1 ".}.
_________
Note: If number that ends with the last 2 (two) digits; in consecutive order; in which, taken as a "separate number" , is evenly divisible by "4" ; then, the entire said number is evenly divisible by "4".
Note: The number given: "1386 " ; ends with: "86" ;
and: " 86 ÷ 4 = 21.5" ; so we know that:
"1386" is not evenly divisible by "4".
_________
Note: If a number ends with the digit: "5" ; or "0" ; then the number is evenly divisible by: "5" . The number: "1386" ; does not meant either of these criteria.
_________
Note: If a number ends with the digit: "0" ; then the number is evenly divisible by: "10" . The number: "1386" ; does not meant this criterion.
_________
Note: If a number ends with the last 2 (two) digits; in consecutive order; in which, taken as a "separate number" , is evenly divisible by "7" ; then, the entire said number is evenly divisible by "7".
Note: The number given: "1386 " ; ends with: "86" ;
and: " 86 ÷ 7 = 12
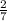 " ; so we know that:
" ; so we know that:
"1386" is not evenly divisible by "7".
_________
Note: If a number ends with the last 2 (two) digits; in consecutive order; in which, taken as a "separate number" , is evenly divisible by "4" ; then, the entire said number is evenly divisible by "4".
Note: The number given: "1386 " ; ends with: "86" ;
and: " 86 ÷ 4 = 21.5" ; so we know that:
"1386" is not evenly divisible by "4".
_________
Note: If a number ends with the last 3 (three) digits; in consecutive order; in which, taken as a "separate number" , is evenly divisible by "8" ; then, the entire said number is evenly divisible by "8".
Note: The number given: "1386" ; ends with: "386" ;
and: " 386 ÷ 8 = 28
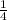 " ; so we know that:
" ; so we know that:
"1386" is not evenly divisible by "8" ;
_________
Since: we know that "1386" is evenly divisible by "9" ;
and "9" is a perfect square;
{since: " 3² = 3 * 3 = 36 " ; and since: "
![\sqrt[]{9} = 3](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/unkxo5qwc5j3f0q3l1gh.png) " }.
" }.
Let's see what the other factor of "1386" is when "9" is a factor:
" 1386 ÷ 9 = 154 " ;
_________
So: √(154) ;
= √9 * √(154) ;
= 3 * √(154) ;
Let's look at the factors of 154:
_________
⇒ 1 & 154; 2 and 77;
List this factors of "154" as: 1, 2, 77, 154;
→ none of which are "perfect squares" ;
→ So, the answer is: "
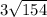 " ;
" ;
or: further calculate with a calculator:
→ "

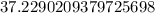 " ;
" ;
→ round to: " 37.229 ".
_________
Hope this is helpful. Best wishes!
_________