Question

The graph of f of x equals x squared is shown. A transformation is applied to f of x resulting in the function g of x equals x squared plus 2. Which graph shows g of x?Answer options with 4 options.F of x is a parabola with a vertex at (0, 0) that opens up. G of x is a parabola with a vertex at (2, 0) that opens up.C.F of x is a parabola with a vertex at (0, 0) that opens up. G of x is a parabola with a vertex at (0, negative 2) that opens up.B.F of x is a parabola with a vertex at (0, 0) that opens up. G of x is a parabola with a vertex at (0, 2) that opens up.D.F of x is a parabola with a vertex at (0, 0) that opens up. G of x is a parabola with a vertex at (negative 2, 0) that opens up.

Answer 1

f(x) is a parabola with a vertex at (0, 0) that opens up

g(x) is a parabola with a vertex at (0, 2) that opens up

Explanation:

Quadratic equation:
`y = ax^2 + bx + c`

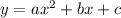
The graph of a quadratic equation is a parabola. The value of
`a`determines its orientation.

If
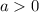`a>0` then the parabola opens upwards and its vertex is its minimum point.

If
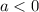`a<0` then the parabola opens downwards and its vertex is its maximum point.

Given:

• f(x) = x²
• g(x) = x² + 2

⇒ g(x) = f(x) + 2

So the transformation of f(x) to g(x) is an upward shift of 2 units, or

a translation of f(x) by the vector
`\left(\begin{array}{ccc}0\\2\end{array}\right)`.

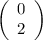Therefore, the y-coordinate of the vertex of g(x) will be 2 units more than the y-coordinate of the vertex of f(x).

Therefore,

• f(x) is a parabola that opens upwards with a vertex at (0, 0)
• g(x) s a parabola that opens upwards with a vertex at (0, 2)