Answer:
A. (-15, -5)
C. (3, 2)
E. (21, 8)
Explanation:
From inspection of the graph, two points on the line are:
Substitute the two points into the slope formula:
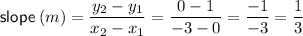
Substitute the slope and the y-intercept into the slope-intercept formula to create an equation of the line:
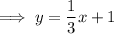
To determine which of the given points are solutions to the graph, substitute each x-value into the equation and compare with the the y-value of the solutions.
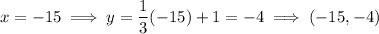
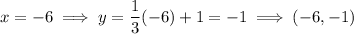
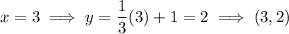
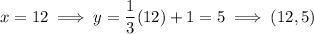
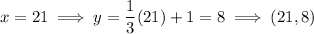
Therefore, the solutions to the graph are:
- A. (-15, -5)
- C. (3, 2)
- E. (21, 8)