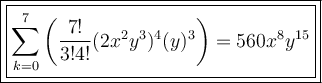Question

Which expression correctly shows how to use the binomial theorem to determine the 4th term in the expansion of (2x²y³ + y)²?

Answer 1

`\textsf{D)} \quad\displaystyle \sum^(7)_(k=0)\left((7!)/(3!4!) (2x^2y^3)^(4)(y)^(3)\right)=560x^8y^(15)`

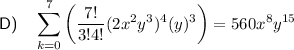
Explanation:

The general form of the binomial theorem is given by:

`\boxed{\begin{array}{c} \underline{\sf Binomial\; Theorem}\\\\\displaystyle (a+b)^n=\sum^(n)_(k=0)\left(\binom{n}{k} a^(n-k)b^(k)\right)\\\\\\\textsf{where}\;\displaystyle \binom{n}{k} = (n!)/(k!(n-k)!)\\\end{array}}`

For the given expression (2x²y³ + y)⁷:

• 
  `a=2x^2y^3`

• 
  `b=y`

• 
  `n=7`

Substituting these values into the binomial theorem, we get:

`\displaystyle (2x^2y^3+y)^7=\sum^(7)_(k=0)\left(\binom{7}{k} (2x^2y^3)^(7-k)(y)^(k)\right)`

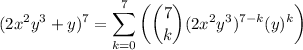
As the first term corresponds to k = 0, then the 4th term corresponds to k = 3, so we can determine the 4th term by substituting k = 3 into the equation:

`\displaystyle \sum^(7)_(k=0)\left(\binom{7}{3} (2x^2y^3)^(7-3)(y)^(3)\right)`

`\displaystyle \sum^(7)_(k=0)\left((7!)/(3!(7-3)!) (2x^2y^3)^(4)(y)^(3)\right)`

`\displaystyle \sum^(7)_(k=0)\left((7!)/(3!4!) (2x^2y^3)^(4)(y)^(3)\right)`

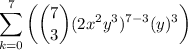
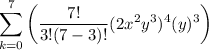
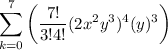
Therefore:

`\begin{aligned}\displaystyle \sum^(7)_(k=0)\left((7!)/(3!4!) (2x^2y^3)^(4)(y)^(3)\right)&=(7*6*5*4*3*2*1)/(3*2*1*4*3*2*1) (2)^4(x^2)^4(y^3)^(4)(y)^(3)\\\\&=(7*6*5)/(3*2*1) \cdot 16x^8y^(12)y^3\\\\&=(210)/(6) \cdot 16x^8y^(15)\\\\&=35 \cdot 16x^8y^(15)\\\\&=560x^8y^(15) \end{aligned}`

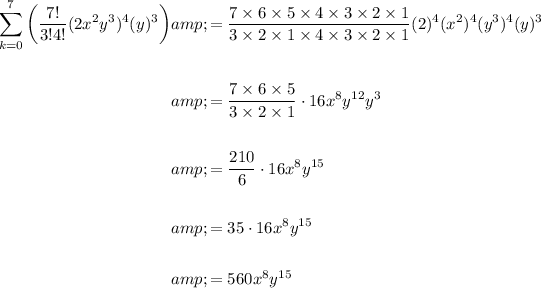
Therefore, the expression that correctly shows how to use the binomial theorem to determine the 4th term in the expansion is:

`\large\boxed{\boxed{\displaystyle \sum^(7)_(k=0)\left((7!)/(3!4!) (2x^2y^3)^(4)(y)^(3)\right)=560x^8y^(15)}}`