Answer:
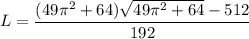
Explanation:
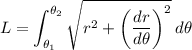
Length of polar curve has formula of:
From power rule, we know that:
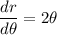
Therefore, substitute r, angles and its derivative in:
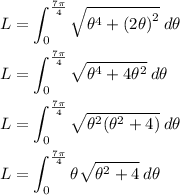
Let the following:
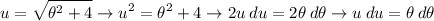
Therefore, substitute in appropriate terms:
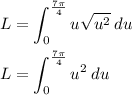
Since we now use u-term as the interval, we have to substitute theta intervals in
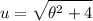 to find new intervals. Hence:
to find new intervals. Hence:
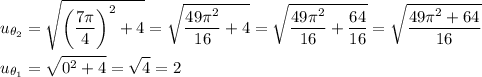
Now we have our new interval of:
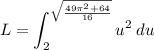
Then we can apply definite integration rule:
![\displaystyle{L = \left[ (u^3)/(3)\right]_(2)^{ \sqrt{(49\pi^2+64)/(16)} } }\\\\\displaystyle{L= \frac{\left(\sqrt{(49\pi^2+64)/(16)\right)^3} }{ 3} - (2^3)/(3)}\\\\\displaystyle{L=\frac{(49\pi^2+64)/(16)\sqrt{(49\pi^2+64)/(16)}}{3}-(8)/(3)}\\\\\displaystyle{L=((49\pi^2+64)/(64)√(49\pi^2+64))/(3)-(8)/(3)}\\\\\displaystyle{L=((49\pi^2+64)√(49\pi^2+64))/(192)-(8)/(3)}](https://img.qammunity.org/2023/formulas/mathematics/high-school/tpv4wai5dhdyn0bke3kds4388ob3vejk5v.png)
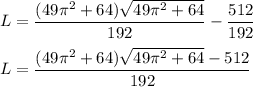
And that’s the answer!