Answer:
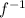 (x) =
(x) =
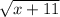 + 4, x=-11
+ 4, x=-11
Explanation:
y = x^2 - 8x + 5, x<=4
x = y^2 - 8y + 5, y<=4 ==> switch the x and y variables to find the inverse
x = y^2 - 8y + 5 ==> solve for y
x + 16 = y^2 - 8y + 16 + 5 ==> add 16 to get a perfect polynomial square
x + 16 = (y - 8/2)^2 + 5 ==> simplify
x + 16 = (y - 4)^2 + 5
x + 16 - 5 = (y - 4)^2 + 5 - 5 ==> isolate y by subtracting 5 on both sides
x + 11 = (y - 4)^2 ==> simplify
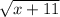 =
=
 ==> take the square root of both sides to remove the
==> take the square root of both sides to remove the
square
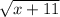 = y - 4
= y - 4
y =
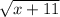 + 4 ==> add 4 on both sides to isolate y
+ 4 ==> add 4 on both sides to isolate y
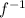 (x) =
(x) =
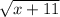 + 4 ==> substitute
+ 4 ==> substitute
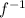 (x) for y
(x) for y
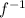 (x) =
(x) =
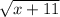 + 4,
+ 4,
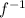 (x)<=4 ==> add in the domain restriction
(x)<=4 ==> add in the domain restriction
4 =
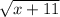 + 4 ==> plugin the domain restriction for
+ 4 ==> plugin the domain restriction for
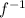 (x)
(x)
0 =
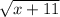 ==> subtract 4 on both sides
==> subtract 4 on both sides
x + 11 = 0 ==> the square root of 0 is 0
x = -11 ==> subtract 11 on both sides
Hence, answer is:
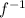 (x) =
(x) =
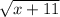 + 4, x=-11
+ 4, x=-11