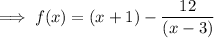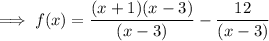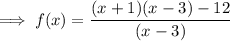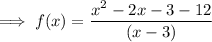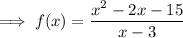1 Answer

Sarvasana · Answer 1 · 2023-09-15T01:05:31+0000

Answer:

f(x) = (x^2-2x-15)/(x-3)

Explanation:

The graph of a function with a slant asymptote y = a and a vertical asymptote at x = b can be written as follows:

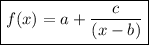
$\boxed{f(x) = a + (c)/((x - b))}$

where c is a constant to be determined using the fact that f(d) = 0 where the function has a zero at x = d.

Given:

Therefore:

f(x) = (x+1) + (c)/((x - 3))

f(-3)=0

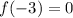
Substitute x = -3 into the function, set it zero, and solve for c:

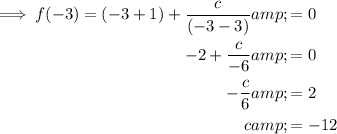
$\begin{aligned}\implies f(-3) = (-3+1) + (c)/((-3 - 3))&=0\\ -2+(c)/(-6)&=0\\-(c)/(6)&=2\\c&=-12\end{aligned}$

Substitute the found value of c into the equation and simplify:

$\implies f(x) = (x+1) - (12)/((x - 3))$

$\implies f(x) = ((x+1)(x-3))/((x-3)) - (12)/((x - 3))$

$\implies f(x) = ((x+1)(x-3)-12)/((x-3))$

$\implies f(x) = (x^2-2x-3-12)/((x-3))$

$\implies f(x) = (x^2-2x-15)/(x-3)$

Please log in or register to add a comment.